WORK IN PROGRESS
This will be continuously expanded to cover:
- questions on many topics
- questions grouped by different theory topics
- video explanations
We will add 100s of questions and 10s of videos as we expand this framework. We aim to continuously expand this before the Kangaroo maths competition in April.

An introduction to
Maths Competitions
A tutorial with examples
Our research has shown that many who are unfamiliar with maths competitions find them daunting and an unnecessary distraction that they can easily avoid. We will cover the important role they can play, and argue that they are not superfluous but a great way to develop a love of maths and an understanding of the usefulness of maths.
We also offer test strategies and preparation material as well as details regarding common maths competitions held in South Africa. Those that use the preparation material will greatly benefit.
Why maths competitions?
Need motivation, a reason why?
Maths matters and improves lives
Maths develops skills that are useful throughout life, helping you to make sense of the world, gain access to education and skills training opportunities that will help you land a great job and help you deal with challengs encountered in daily life.
Many learners find maths to be unrelated to their life. These problem solving questions build a bridge between the maths concepts studies and the questions they face in life.
Benefits of maths competitions
The benefits of maths competitions include:
1 fun - learners can get a fun maths experience
2 confidence building
3 showing real world application that can help to show that maths is useful in daily life
4 competition has the potential to bring the best out of learners who can spend time preparing and participating (with all this time being time well spent building mathematical competencies)
Problem solving complements the sylabus
The most important function of schooling is to prepare you for life in the real world. Getting good marks is just a way of measuring your preparedness, and your competence in a range of areas.
Having the ability to applying the theoretical/abstract mathematical principles mastered in school to solve real life problems is the true test of mastery.
Many of the questions found in maths competitions build a bridge from maths theory to the real world, and learners who engage with them will be better prepared.
You get what you measure. If you measure outomes according to the syllabus, you will get teachers and learners that focus on the syllabus.
Many teachers shy away from focusing on anything other than the curriculum, and avoid problem solving questions despite these being what builds a bridge from the mathematica theory to something applicable to their lives.
Be prepared - more is better
The motto of the Boy Scouts is to Be Prepared.

Not just the scouts - the military, everyone knows. Preparation is a legal way to get ahead.
Some see cheating as a way to get ahead, but this is unethical and doesn't help you in life.
You should think of preparation and practice as being a legal way to get ahead of the rest of the competition.
Practice will make you seem luckier
Gary Player is one of the most successful golfers. He is famous for this quote:

Gary does not think that he actually gets luckier as a result of practice, but what he does mean is that it when he practices, it seems like he is getting luckier. Importantly, he is rewarded for his efforts, and is encouraged to do more practice.
Mathematicians - like sportsmen - benefit from practice. In solving questions you will be building or reinforcing your mathematical toolbox that you will be able to reuse in future.
Getting to see a question that you have seen before - even just a similar question - is an added bonus.

1000's of problems are available on MyTutor.chat - a free service that ensures that the questions you are given are suited to your level and ability.
Finding it all daunting?
This quote from Bishop Tutu may help put things in perspective:

Sometimes the only way to deal with a daunting and seemingly insurmountable problem is one small step at a time. When you take the step, you may not feel like you have made progress, and may still be discouraged by the long way you have to go.
If you think back to when you were learning to read for the first time, you found it overwhelming, slow and diffcult, but now, reading comes naturally and without much effort. You have gained new skills and competencies, and every time you read you practice that part of your brain and get better at it.
Improving mathematics involves being introduced to new concepts, and then learning how to apply that type of mathematical thinking.
Problem solving questions - the kinds of problem that you will find on MyTutor.chat are a great way to introduce mathematical techniques, and to show how mathematical tools can be used to solve real world problems.When it comes to mathematics, there are many ways you can be introduced to new topics, and you can reinforce your understanding and ability to apply the concepts by using them.
Fun problems that teach
Here are a few playful problems that introduce the more than a thousand that are available on MyTutor.chat:
Wondering where to start? Why not here?

1000's of problems are available on MyTutor.chat - a free service that ensures that the questions you are given are suited to your level and ability.
There are plenty more questions where these three came from - you will find them all over this page, and more than a thousand at MyTutor.chat.
Want some question and answer videos?
We have started to build a video library, and here are some examples:
There are plenty more videos where these three came from and we hope to have a few hundred in 2023.
Test strategy
Tips and tricks to help you
Time management - get the most from the time available
These tests are designed to not be finished in the available time.
Ditch questions and move on.
Pace yourself.
Mark allocation including negative marking
Find out about the mark alloction in advance. It is common to have different types of questions that are allocated different marks per question type.
A common approach is for the questions to be classified as being either easy, medium or difficult, and having the easy questions earn the least points, and having the difficult questions earning the most.
Negative marking
When there is no negative marking, it is very important that you answer all questions, even if this means guessing in the last minute. This is because you may guess some of the questions right, and if you do, you will earn additional points.
Workng through these questions will deepen your understanding of negative marking:
Exclude options - and guess
If you can show that all but one of the answer options are incorrect, you will have identified the correct answer. This can be a short cut, and is often the fastest approach to identifying the correct solution.
If you can exclude some options that are clearly incorrect, you can increase the chance of getting the correct answer.
If you can identify a property of the correct answer -say if the answer is positive or negative, even or odd - you can rule out the answer options that don't have that property.
Play to your strengths
If you know that you are good at particular types of question, try and answer them first.
If you are battling with a question, sometimes the bet strategy is to move on to the next one where you have a better chance of earning points.
Useful theory
Spend time here building skills
Definitions - primes, whole numbers, integers etc
Some questions rely on knowledge of certain terms.
Here are some examples:
The natural numbers are:
1; 2; 3; 4; 5; ...
The whole numbers are:
0; 1; 2; 3; 4; 5; ...
The integers are:
...; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; ...
The integers are split into those that have 2 as a factor and those that don't. Those that have 2 as a factor are called even numbers:
...; -8; -6; -4; -2; 0; 2; 4; 6; 8; 10; ...
Even numbers can be written as 2n where n is an integer.
The integers that do not have 2 as a factor are called odd numbers:
...; -9; -7; -5; -3; -1; 1; 3; 5; 7; 9; ...
Odd numbers can be written as 2n+1 where n is an integer.
A fraction consists of one number divided by another. The number on top is called the numerator, and the number below is called the divisor:

Prime numbers
A prime numbers is a whole number greater than 1 that cannot be exactly divided by any whole number other than itself and 1.
You should be familiar with the following list of prime numbers that are less than 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
A composite number is a whole numbers greater than one that has more than two factors. All natural numbers are either prime numbers or compund numbers.
Here are some composite numbers, and their factors:
4: 1, 2, 4
6: 1, 2, 3, 6
8: 1, 2, 4, 8
9: 1, 3, 9
10: 1, 2, 5, 10
Permutations and Combinations
A permutation is a
A combination is a
Squares, Cubes - and other higher powers
You will be advantaged if you are familiar with the squares and cubes and other higher powers of various numbers.
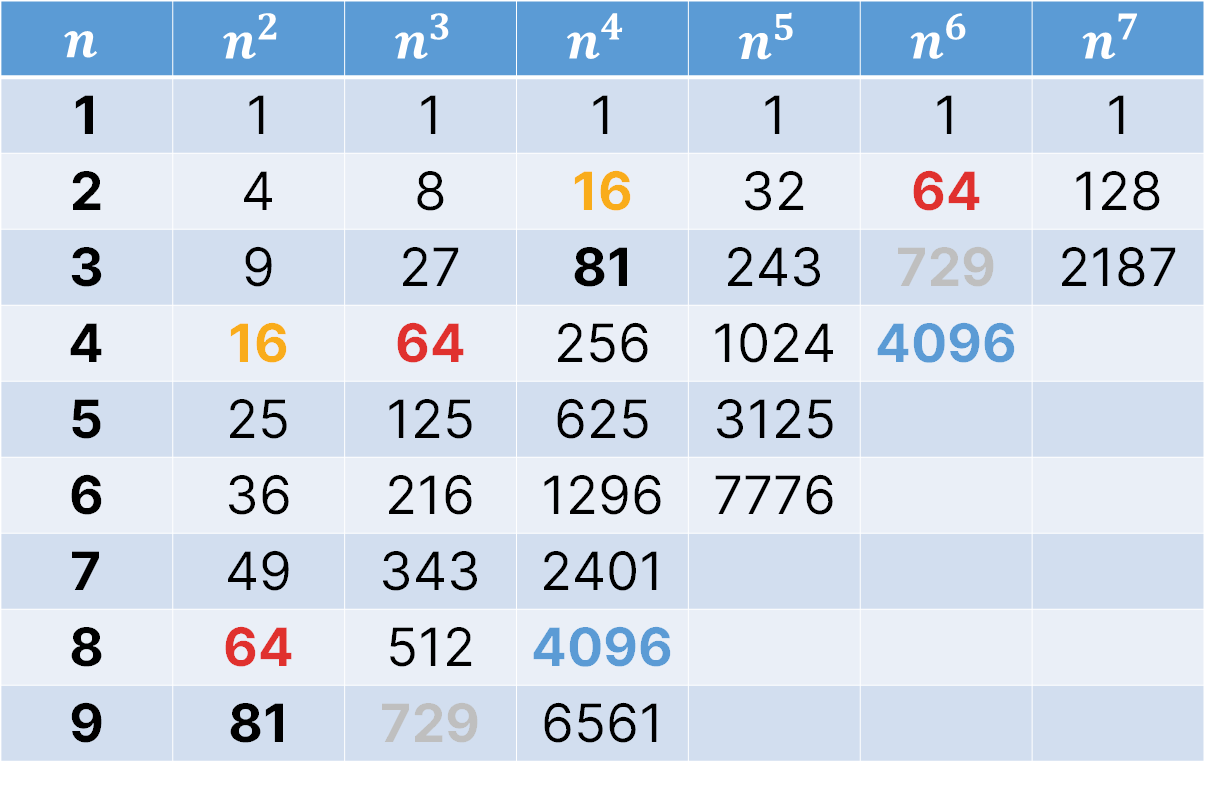
You will be at advantage if you know even more than this, for example the squares of all integers less than 20.
There are more questions available at MyTutor.chat.
Pythagoras - theories and triples
Pythagoras was a Greek mathematician. He noticed that the sum of the squares of the shorter sides of a right angled triangle are equal to the square of the hypoteneuse. This gave rise to a theory that bears his name: Pythagoras's Theorem
The Pythagoras Theorem
The Pythagoras Theorem states that if a triangle is right-angled, then the sum of the squares of the two shorter sides is equal to the square of the hypotenuse - which is the third and longest side.
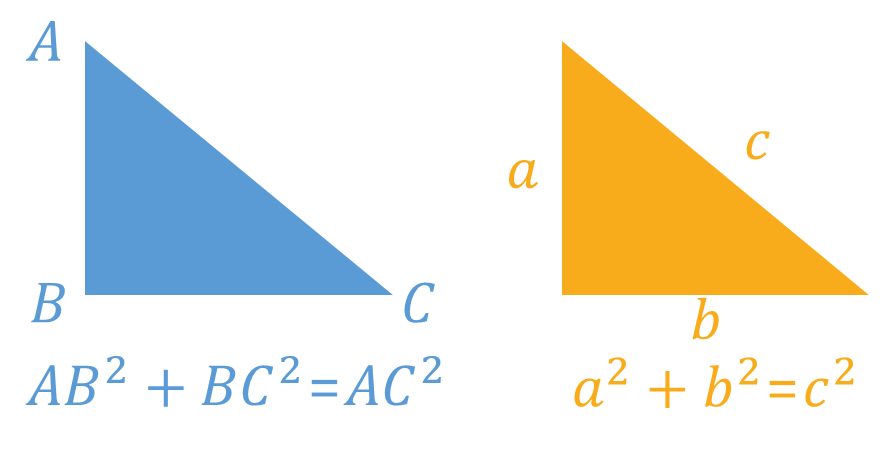
This video shows 6 different proofs:
Phythagorean Tripples
Phythagorean tripples consist of three positive integers a, b, and c, such that
a² + b² = c²
Here are some common tripples that are worth knowing off by heart:

Factorial notation- !
The factorial of a non-negative integer n is denoted as n!, and is the product of all positive integers less than or equal to n or
n!=n×(n-1)×...×2×1
Here are some examples:
1!=1
2!=2×1=2
3!=3×2×1=6
4!=4×3×2×1=24
5!=5×4×3×2×1=120
⋮
n!=n×(n−1)×...×2×1
0!=1
Physical Units - science and maths are related
Physical quantities are measured using various units. Here are some that may be useful:
1 cm³ = 1 ml
1000 cm³ = 1 l
1000 m = 1 km
1000 g = 1 kg
100 cm = 1 m
Mathematics is widely used in physics and other branches of science.
Event Sylabus
(which is always very broad)
SAMF- organisers of the SAMO and SAMC
The South African Mathematics Foundation runs two events:
1 the SAMC - the South African Mathematics Challenge (Grade 4-7) and
2 the SAMO - the South African Mathematics Olympiad (Grades 8-12)
They do not have a syllabus.
Kangaroo sans Frontiers - Kangaroo Without Borders
The Kangaroo sans Frontiers event, in English the Kangaroo Without Borders event, is the world's larges maths competition with >4m entrants from 80 countries. South Africa participated for the first time in 2022, and we are looking for rapid growth in 2023:
1 Pre-ecolier (Grade 1-2)*
2 Ecolier (Grade 3-4)*
3 Benjamin (Grade 5-6)*
4 Junior (Grade 7-8)*
5 Cadet (Grade 9-10)*
6 Student (Grade 11-12)*
* Note: This is just an indication, and any paper can be written. Many in the Southern Hemisphere could regard themselves as being 6 months behind at the time of writing in H1, as those in the northern hemisphere will be in their second half of the school year by then.
Click on the section for the sylabus of that paper:
Pre-Ecolier (Grades 1-2)
The following types of question will come up in the event:
• Counting to 20 and ordering small numbers for 3 and 4 point problems; for 5 point problems can be up to 30
• Comparing sizes (more, less, equal) of small numbers and geometrical regions
• Ordinal numbers
• Place value (ones, tens, and up to hundreds for 5 point problems)
• Simple addition and subtraction should be just for 2 single-digit numbers
• Number line just in simple applications
• Fractions (½, ⅓, ¼), only using the words half, third, quarter
• Ordering objects by applying one specific characteristic; Sorting and classifying objects
• Measurement - length, capacity, weight, temperature, time only with small integers
• Patterns – numerical and geometrical, no sequences to be continued somehow
• Perimeter; comparing length of broken lines
• Relative positions in a figure or in space (behind, in front of, next to, left, right, over, under, middle, in, out)
• Descriptive properties of geometrical figures
• Puzzles with mazes or shapes
• Simple spatial visualization of cubes and cuboids
• More likely, less likely, certain, impossible
• Bars and graphs (pictographs)
• Venn diagrams (easy situations)
• Calendar (week, month, year)
• Money with small numbers
• Clock faces (full and half hours), but no minutes for 3 and 4 point problems
• Simple axial symmetry; rotated shapes
• Pre-algebra ideas like balances with concepts like equal, more, less, ...
Ecolier (Grades 3-4)
In addition to the sylabus for Pre-ecolier - Grade 1 and 2, the following may be covered by this event:
Geometry
• Measurement: simple area and perimeter, for instance comparing lengths, counting in boxes on squared paper
• Symmetry
Numbers
• Basic operations with positive integers (+, -, ×, ÷) with numbers under 1000
• Comparing sizes of numbers; ordering numbers
• Multiples and divisors
• Simple fractions representing parts of figures, like quarter, half and third.
• Number of the year problem can be an exception to the under 1000 rule for problems about the digits or similar ideas
• Averages (arithmetic mean)
Logic
• Strategies for simple games
• Classification of objects
• Puzzles
Benjamin (Grades 5-6)
In addition to the sylabus for Pre-ecolier - Grade 1 and 2 and Ecolier - Grade 3 and 4, the following may be covered by this event:
Geometry – plane geometry
• Points, lines, segments, circles, (special) triangles and (special) quadrilaterals
• Symmetry
• Perimeter and area of squares, rectangles and right triangles
Geometry – solid geometry
• Only problems in solid geometry that allow an intuitive approach
Numbers and algebra
• Calculations with natural numbers
• Recognizing multiples of 2, 3, 5, 9 and 10
• Very easy calculations with positive rational numbers (fractions or decimals)
• Algebraic thinking without the use of formal algebraic notation
• Counting problems that do not involve any formulas
• Problems about decimal number system
• Easy problems with order between numbers (integers, decimal, fractions) and links with their representations (on graduate line, surfaces, …)
• Very easy problems with percentages
• Metric system (length, weight, area, volume, temperature, time)
• Problems using time, distance and/or velocity
Logic
• Logical problems that can be solved
Junior (Grades 7-8)
In addition to the sylabus for Pre-ecolier - Grade 1 and 2, Ecolier - Grade 3 and 4 and Benjamin - Grade 5 and 6, the following may be covered by this event:
Geometry – plane geometry
• symmetry
• Pythagorean theorem
• similarity
• area of simple plane figures
• angle calculations (parallel and normal angles, angles in a circle, angles in triangles and simple polygons)
• circles
• parabola
• rotation, translation, scaling
• point coordinates without computations
• simple regular polygons
Geometry – solid geometry
• spatial relationships
• cubes, prisms, pyramids
• spheres, cones, cylinders
• Platonic solids
• volume
• 3-d movement of one- and two-dimensional objects, i.e. knots, folding, etc.
Number Theory
• number puzzles
• simple usage of powers of numbers
• prime numbers
• use of prime factorisation (low level)
• using digits
• number patterns
• simple Diophantine equations
• very simple modulo calculations, no modulo calculus
Functions, Sequences
• interpreting simple graphs
• simple arithmetic and geometric sequences
• simple functional equations
• simple finite recursions
Algebra
• addition, subtraction and multiplication of polynomials
• powers and roots
• equations, simple quadratic equations
• simple systems of linear equations
• simple inequalities; solutions with sets written as intervals
Combinatorics and Probability
• simple combinatorics as for instance countable permutations
• simple probability without theoretical knowledge
• inclusion/exclusion principle
Logic / Puzzles
Cadet (Grades 9-10)
Geometry – plane geometry
• Point, line, segment, angle, acute angle, right angle, obtuse angle, circle, radius, diameter, triangle, isosceles triangle, equilateral triangle, quadrilateral, square, rectangle, parallelogram, rhombus, trapezium, diagonal, regular polygon
• Symmetry, translation and rotation in the plane
• Sum of the angles of a triangle, sum of the angles of a square, angles formed by two parallel lines intersected by a third line
• Elementary propositions about angles, sides and diagonals in special triangles and quadrilaterals
• Perimeter and area of a square, rectangle, parallelogram, rhombus, trapezium, triangle
• Coordinates of a point in the plane
Geometry – solid geometry
• Cube, regular parallelepiped, prism, pyramid, cone, cylinder, sphere
• Area and volume of a cube and a regular parallelepiped
• 3-d movement of one- and two-dimensional objects (such as knots and folding)
• Intuitive 2-d representation of a 3-d object
Numbers
• Calculations with integers and rational numbers (fractions or decimals)
• Prime numbers
• gcd and lcm
• Recognizing multiples of 2, 3, 4, 5, 6, 9 and 10
• Intuitive knowledge about the divisibility of a sum and a difference
• Powers with exponent 2
• Square root of a perfect square, cubic root of a perfect cube
• Combinatorial problems that do not involve any formulas
• Percentage
• Metric system (length, weight, area, volume, temperature...)
• Problems using time, distance and velocity that do not involve algebraic calculation.
• Problems that involve only an intuitive knowledge of probability
Algebra
• Linear algebraic calculations (adding and subtracting monomials of degree 1, multiplying a rational number and a monomial of degree 1)
• Problems that can be reduced to a linear equation or inequality in one variable.
Logic
• Logic problems that can be solved in a limited number of steps or by analyzing a limited number of cases or hypotheses
Senior (Grades 11-12)
Geometry – plane geometry
• lines, segments, polygons
• congruence and similarity
• symmetry
• Pythagorean theorem
• area of simple plane figures (including those that can be solved by breaking a shape into smaller self-similar shapes)
• angle calculations (parallel and normal angles, angles in a circle, angles in triangles and polygons)
• circles and parabolas
• concurrency, collinearity and concyclicity
• rotation, reflection, translation, homothety (i.e. isometries and similarities)
• regular polygons
Geometry – plane analytic geometry
• point coordinates, equations of the line, the circle and the parabola
• calculating points and lines in the plane
• triangle calculations with trigonometric methods
Geometry – solid geometry
• spatial relationships (chirality/spatial orientation, nets of solids)
• cubes, prisms, pyramids
• spheres, cones, cylinders
• Platonic solids
• point coordinates
• volume
• projections
• 3-d movement of one- and two-dimensional objects, i.e. knots, folding, etc.
Number Theory
• number puzzles
• powers of numbers
• prime numbers
• prime factorisation
• triangular numbers
• Diophantine equations
• divisibility and simple modulo calculations, parity considerations
Functions, Sequences
• interpreting graphs
• simple arithmetic and geometric sequences, other well-defined sequences (e.g. by recursion)
• simple functional equations
Algebra
• absolute value
• powers and roots
• logarithms (only elementary properties, no change of base)
• systems of equations; replacement or change of variables
• simple inequalities; solutions with sets written as intervals
• factorising simple polynomials
• quadratic equations / polynomial equations
• solving worded or situational questions by applying algebraic methods
Combinatorics and Probability
• n! (permutations)
• binomial coefficients; number of subsets
• inclusion/exclusion principle
• systematic counting (by analysing cases)
• calculating with probability trees
Logic / Puzzles
• interpretation of a problem: the possibility of reduction of the problem to another problem in any other subject
• semantics and syntax: inference of facts from partial information in a network of logically connected statements
• models: puzzles created from a specific set of axioms and/or rules
• language structure
• Boolean problems (e.g. truth-tellers and liars)
Note: Many of the questions are not syllabus related, and while no content is specifically required, some the questions vary in difficulty and are better suited to different ages.
For more information contact MyTutor.chat.
